Vedic Math
By The Edge Learning Center
Vedic Mathematics is an ancient Indian Mathematical system. It was given the name when it was rediscovered from the Vedas (Sacred texts of Hinduism also known as Indian Sankrit texts) during the years 1911—1918 by Sri Bharati Krsna TIrhaji (1884-1960). His research during these years claimed that all mathematics is based on the sixteen sutras or word-formulae which can be used for problems in all areas of mathematics, including arithmetic, algebra, geometry, calculus, and comics.
‘Vedic Mathematics deals mainly with various Vedic Mathematical formulae and their applications for carrying out tedious and cumbersome arithmetical operations and to a very large extent’ Tirthaji, B. K. (1965 p.xvii).
Bharati Krsna, born 14th March 1884, was a gifted scholar in science and humanities, but his background showed his main focus was on mathematics. He was also noted for having the ability to speak English fluently and his admirable academic record of a Masters degree in six subjects. Despite his abilities and numerous accolades, Bharati Krsna is most famously known for his rediscovery of the Vedic Mathematical System. Throughout his lifetime, he was able to write sixteen volumes on this mathematical system, but they were unfortunately all lost. However, in the last few years of his life, before his passing at the age of 75, he was able to write a book called Vedic Mathematics, which was finally published five years after his death.
| The Sixteen Sutras | |||
|---|---|---|---|
| 1 | Ekadhikena Purvena (Corollary: Anurupyena) Meaning: By one more than the previous one | 9 | Chalana-Kalanabyham (Corollary: Antyayoreva) Meaning: Differences and Similarities |
| 2 | Nikhilam Navatashcaramam Dashatah (Corollary: Sisyate Sesasamjnah) Meaning: All from 9 and the last from 10 | 10 | Yaavadunam (Corollary: Samuccayagunitah) Meaning: Whatever the extent of its deficiency |
| 3 | Urdhva-Tiryagbyham (Corollary: Adyamadyenantyamantyena) Meaning: Vertically and crosswise | 11 | Vyashtisamanstih (Corollary: Lopanasthapanabhyam) Meaning: Part and Whole |
| 4 | Paraavartya Yojayet (Corollary: Kevalaih Saptakam Gunyat) Meaning: Transpose and adjust | 12 | Shesanyankena Charamena (Corollary: Vilokanam) Meaning: The remainders by the last digit |
| 5 | Shunyam Saamyasamuccaye (Corollary: Vestanam) Meaning: When the sum is the same that sum is zero | 13 | Sopaantyadvayamantyam (Corollary: Gunitasamuccayah Samuccayagunitah) Meaning: The ultimate and twice the penultimate |
| 6 | (Anurupye) Shunyamanyat (Corollary: Yavadunam Tavadunam) Meaning: If one is in ratio, the other is zero | 14 | Ekanyunena Purvena (Corollary: Dhvajanka) Meaning: By one less than the previous one |
| 7 | Sankalana-vyavakalanabhyam (Corollary: Yavadunam Tavadunikritya Varga Yojayet) Meaning: By addition and by subtraction | 15 | Gunitasamuchyah (Corollary: Dwandwa Yoga) Meaning: The product of the sum is equal to the sum of the product |
| 8 | Puranapuranabyham (Corollary: Antyayordashake’pi) Meaning: By the completion or non-completion | 16 | Gunakasamuchyah (Corollary: Adyam Antyam Madhyam) Meaning: The factors of the sum is equal to the sum of the factors |
By one more than the previous one (1st Sutra): Squaring numbers ending in 5
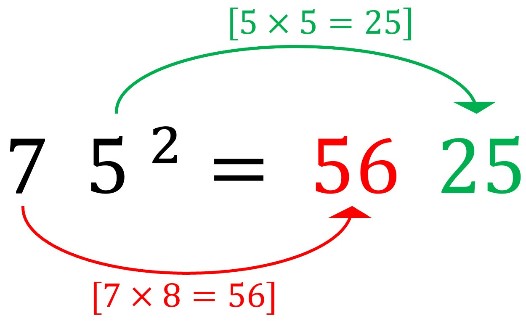
e.g. 75² = 5625
There are two parts to this answer 56 and 25.
1) The first half of the answer is the product of the first digit and ‘one more’ than it: [7 x 8 = 56]
2) The second half, however, will always end with 25: [5 x 5 = 25]
Multiplying numbers where the first digits are the same and the last digits add up to 10
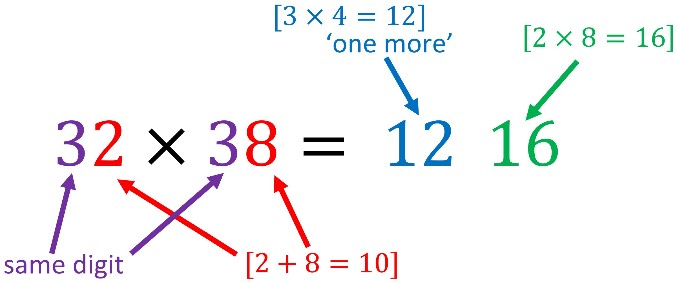 e.g. 32 x 38 = 1216
e.g. 32 x 38 = 1216
There are two parts to this answer 12 and 16.
1) The first half of the answer is the product of the first digit and ‘one more’ than it: [3×4=12]
2) The second half is the product of the last digit of the multiplicand and multiplier: [2×8=16]
If the product is a single digit answer, i.e. 1×9=9, then it should be written as a two-digit number 09.
Therefore, 81×89=7209.
All from 9 and the last from 10 (2nd Sutra): Used for instant subtraction
As the name implies, every digit is subtracted from 9 except for the last, which is subtracted from 10. This method will always work for subtraction from any number consisting of a 1 followed by zeros, i.e. 100, 1000, 10000 etc.
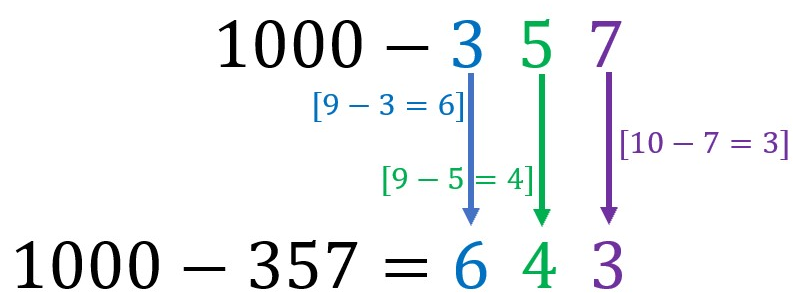
If we have 1000 subtracting a 2-digit number, however, we place a zero in front of the first digit. For example, for 1000-83 we will treat it as 1000-083, and therefore the answer will be 917.
Vertically and crosswise (3rd Sutra): You do not need to multiply beyond 5×5
This is a particularly useful trick for individuals who struggle to learn their times tables.
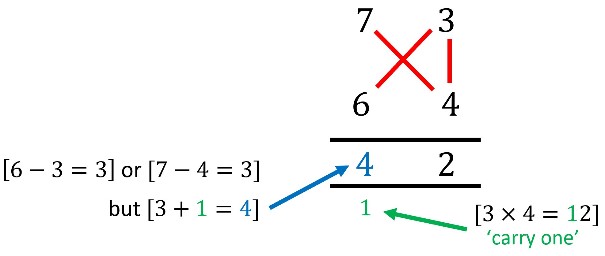
e.g. 8 x 7 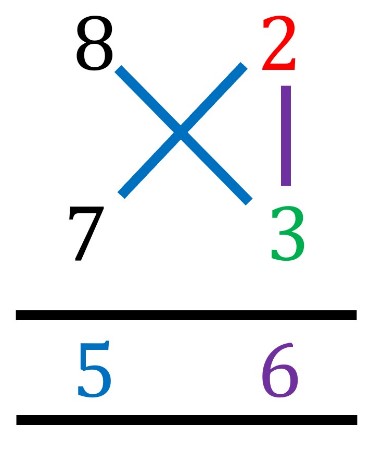
1) Place the multiplicand and the multiplier in the left-hand column
2) In the right-hand column, you write the difference between itself and 10. [10-8=2] and [10-7=3]
3) Subtracting crosswise will give you the first digit of the answer, so either [7-2=5] or [8-3=5]
4) The next digit is made by multiplying the numbers on the right-hand side [2×3=6]
If the answer of the last digit is greater than 9, you have to ‘carry over’. For example:
A ‘graceful’ method to multiply 2-digit numbers
More commonly known as Long Multiplication; however, we can actually write the answer straight away without all the steps using the ‘Vertically and Crosswise Formula’
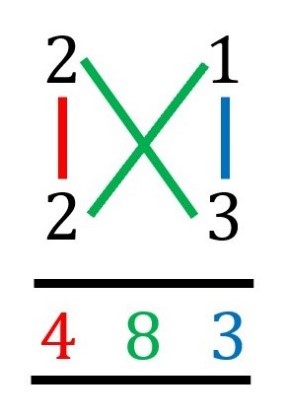
e.g. 21 x 23
There are 3 steps:
1) First multiply vertically on the left; the product is the first digit of the answer: [2×2=4]
2) Multiply crosswise and add the products; the sum is the middle digit of the answer: [(2×3)+(2×1)=8]
3) Finally multiply vertically on the right; the product is the last digit of the answer: [1×3=3]
Multiplying numbers close to 100
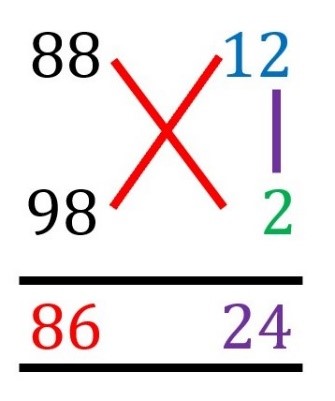
e.g. 88 x 89
1)Find the difference between each number and 100. [100-88=12] and [100-98=2]
2)For this method, instead of crosswise multiplication, you subtract the difference. The difference will be the first digits of your answer. It does not matter which one you choose to subtract as the answer should be same. [88-2=86] “or” [98-12=86]
3)The last digit comes from the product of the differences. [12×2=24]
Multiplying numbers just over 100
e.g. 103 x 104
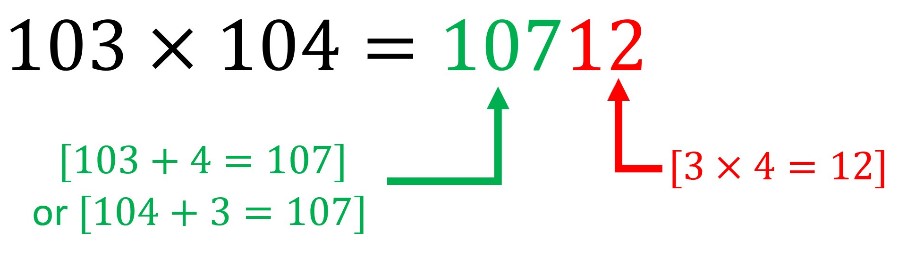
There are two parts to this answer 107 and 12.
1) The first half of the answer is the sum of the first number and the last digit of the second, or vice versa: [103+4=107] or [104+3=107]
2) The second half of the answer is the product of the last digit of the multiplier and the multiplicand: [3×4=12]
A ‘trick’ for multiplying by 11
e.g. 26 x 11 = 286
1) You leave the multiplicand alone and they make up the first and last digits of the answer, 2 and 6 respectively.
![]()
2) The middle digit(s) is the sum of the digits of the multiplicand. Therefore, the middle digit is 8.
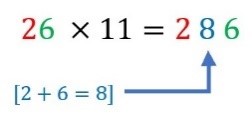
An easier way for dividing 2-digit numbers by 9
e.g. 23 ÷ 9
1) The first digit of the dividend will be the answer.
![]()
2) The remainder is the sum of the digits in the dividend.
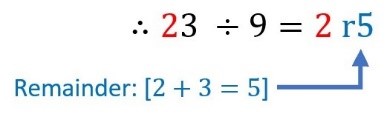
If the sum of the 2 digits is greater than 9, you will have to carry over the number, BUT remember we are working in terms of 9, so you must compensate for carrying ‘10’ over by adding 1 back to the remainder.
e.g. 48 ÷ 9
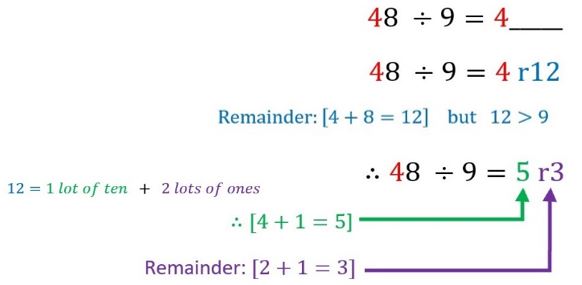
Vedic Mathematicsis a mathematical system or collection of techniques which allows us to solve difficult and large number calculations in a quicker and easier way. While many mathematicians have argued that many of these ‘tricks’ are dependent on specific numbers, there still are benefits to studying Vedic Mathematics, such as the techniques allowing us to do calculations ten times faster. Also, these methods can allow children to develop an interest in and eradicate their fear of math.
About The Edge
The Edge Learning Center is Hong Kong’s premier Test Preparation, Academic Tutoring, and Admissions Consulting services provider. Founded in 2008, The Edge has helped thousands of students improve their ACT and SAT scores as well as their IB and AP grades. The AC team has just finished off another successful period in which students gained acceptance to schools such as Columbia, Yale, UChicago, UPenn, Oxford, and more! Check out our latest Admissions Results!

