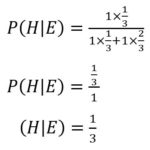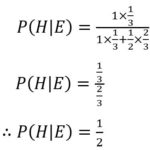Monty Hall Problem

By Tracy Man

(Mathematics & School/University Entrance Exam Tutor)

Suppose you are on a game show and given a choice of three doors. Behind one door is the grand prize of a brand-new car and behind the remaining two doors are goats. Say you pick door no.1; the host examines the other two doors and picks door no.3, which has a goat. The host will now ask you, ‘Would you like to pick door no.2 instead?’

 

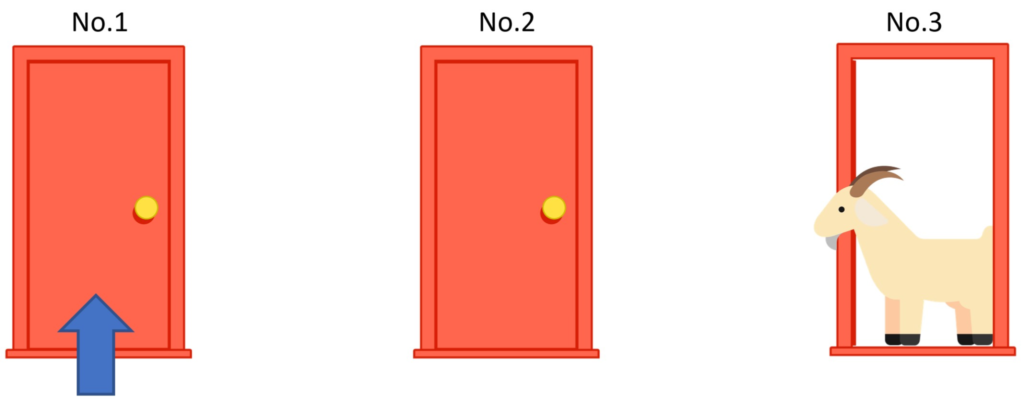
Here is the problem: Should you stay or switch?

This is a famous probability based and paradoxical brain teaser that has been seen on numerous game shows, where it was first presented on a then famed American show called ‘Let’s Make a Deal’ in 1975. This problem was coined after the game show host, who first posed this question to his contestants, Monty Hall.

In the same year that this problem was first introduced, Steve Selvin wrote a letter to American Statistician, to explain how this problem could be solved using probability and, despite what many would think, that switching would be a more advantageous choice. Years later Marilyn vos Savant also responded to one of readers who asked the same problem, in her Parade magazine in 1990, that changing their selection is the better option.

However, this solution is based on certain assumptions about how the player and host choose their doors i.e. the player will pick door one and the other door opened is not random. The outcome is also dependent on the following additional conditions:

1. The host always opens a door not chosen by the player.
2. The door opened by the host must have a goat behind it and not a car.
3. The host must give the player the option to switch doors.

The answer can be explained by the placement of the goats and using simple probability to count all the possible outcomes. The player a ²⁄₃ chance of picking a goat on his or her first choice. Even after the host opens the door with the other goat behind it, this probability does not change. Since the contestant has a higher probability of picking a goat at the start and the host will always reveal the second goat, there is a ²⁄₃ chance that if he or she switches doors, he or she will win the car.

The solution can also be illustrated by showing all the possible outcomes.

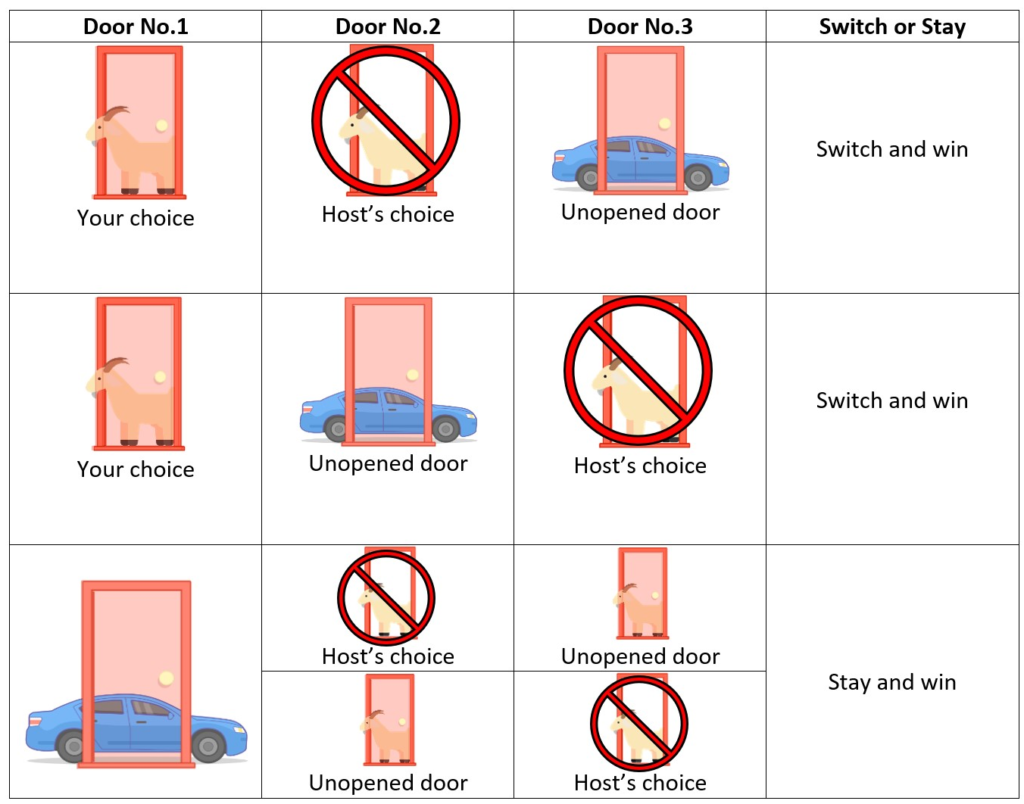
As the diagram above shows, switching doors would by a better option as the player has, overall, a ²⁄₃ chance of winning the car. Whereas staying with their original choice only gives them a ¹⁄₃ chance to win. As mentioned before, there is a greater probability of picking a goat at the start and the host is guaranteed to open a door with a goat behind it, so, as a result, the participant doubles their chance of winning by switching doors.

Bayes’ Theorem and Conditional Probability

Even though there have been many mathematicians, who overtime, have proven that the solution above is correct, numerous people and influential mathematicians such as Paul Erdős struggled to believe that this solution was correct. The main aspects that many have not been able to understand and questions are:

• Why are the odds not 50-50 after the host has opened the second door?
• Why does switching the doors mean that the contestant now has a ²⁄₃ chance of winning the car and staying with their initial choice is only ¹⁄₃ ?
• If the door opened by the host was random and showed a goat, why are the odds of switching vs staying are now 50-50?

All the above questions can be answered by Bayes’ Theorem. It is a formula, derived from conditional probability, that describes how to update probabilities of hypotheses when given 𝙃 and evidence 𝙀, Bayes’ Theorem states that the relationship between the probability of the hypothesis before receiving the evidence 𝙋(𝙃|𝙀) is:

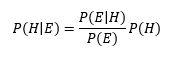
Now applying this formula to our given scenario, we know that every door has either a car or a goat behind it, and so the hypothesis “notH” or (H’) is equivalent to “door no.1 has a goat behind it”. Therefore, Bayes’ Theorem states that:

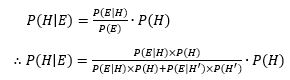
As the problem states that the host examines the remaining doors and intentionally open a door with a goat behind it, we can break down the component as the following:

• P(H) = ¹⁄₃ This is the prior probability that door no.1 has a car behind it without knowing about the door the host will reveal.
• P(H¹)= 1-P(H) = ²⁄₃. This is the probability that the contestant does not initially pick the door with a car behind it.
• P(E|H)=1. This is the probability that the host will open a door with a goat behind it given that there is a car behind door no.1. Since the host always shows a door with a goat behind it, the probability is 100%.
• P(E│H¹)=1. This is the probability that the host will open a door with a goat behind it given that there is a goat behind door no.1. Again, since the host always shows a door with a goat behind it, the probability is 100%.

 

If we now substitute all of the information into the formula, we can calculate P(H│E):

The probability that the car is behind door no.1 is the not affected by the evidence. However, since the car can only be behind either door no.1 or the door unopened by the host, the probability that the car is behind the unopened door is ²⁄₃. Therefore, switching doors will double your chances of winning the car compared to staying with your initial choice.

The Random Monty Hall Problem

The result for this scenario crucially depends on the host opening a different door from the participant and always has a goat behind it, irrespective of which door was picked first by the participant, P(E│H)=P(E|H¹). But what would happen if the host randomly opened a door the player did not pick and had a goat behind it? What is the probability that the contestant’s first choice is correct, regardless of what number door they chose? Then, in this case:

• P(E│H)=1 This is the probability that the host will open a door with a goat behind it given that our first selection has a car behind it. If the player has already chosen the car, then there are only goats left behind the remaining doors and the host has a 100% chance of opening a door with a goat behind it.
• P(E│H¹) = ¹⁄₂. This probability changes, unlike the previous scenario. The chance of the host choosing a door with a goat behind it given that the player’s initial choice had a goat behind it. If the host now selects a door randomly between a door which has a goat behind it or a door that does not have a goat behind it (i.e. the car), he has a 50% of choosing a door with a goat behind it.

If we substitute this information into the formula:

Therefore, there is 50% chance that the contestant’s initial pick is correct when the host randomly opens a door and has a goat behind it.

The Monty Hall problem is mathematically similar to the earlier ‘Three Prisoners Problem’ and ‘Bertrand’s Box Paradox’

Sign up a trial lesson with Tracy now!

---

About The Edge

The Edge Learning Center is Hong Kong’s premier Test Preparation, Academic Tutoring, and Admissions Consulting services provider. Founded in 2008, The Edge has helped thousands of students improve their ACT and SAT scores as well as their IB and AP grades. The AC team has just finished off another successful period in which students gained acceptance to schools such as Columbia, Yale, UChicago, and more! Check out our latest Admissions Results!