How to Approach Optimization Questions in Calculus

By The Edge Learning Center

If you are studying math under IBDP, AP, or taking additional math in IGCSE, chances are you will be learning about calculus. At first, the concept of calculus seems very daunting: how do we measure changes when it is so miniscule that it is almost nothing? As abstract as the premise sounds, calculus is one branch of mathematics that can be found in many other fields.

Optimization is one of the first real-life applications in calculus that most students will learn. After students learn about the various tools and rules to take the derivative of a function on the xy-plane, they will start learning about applying the skills to “optimize” a given situation. The process of optimization generally involves either finding the minimum or the maximum. Imagine a company trying to decide how many new items they should manufacture next year: make too little, and they may not be able to sell enough to make money; make too much, and the surplus may end up costing the company. To find the “sweet spot”, we can use calculus to help us optimize the profit based on the amount of units to be manufactured.

In reality, though, these problems are much more complicated than the scenario mentioned above; the company will also need to consider the demand, logistics, manufacturing cost, and so on, before making a sound decision. But before we can tackle a complex system like this, we need to learn about the basic first. A simple function with one independent and one dependent variable is what you will be focusing on at this level.

Before getting into the details, let us review a few terms. A function is a relationship. We generally think of a function as inputting x to get the y value. That is true if we are considering a graph. Any relationship that provides a unique output given an input is a function. For optimization, our first job is to identify the input and output.

The inputs and outputs are generally referred to as independent and dependent variables, respectively. A complex system can, and will, end up having multiple inputs and/or outputs. At our current level, we will only be able to deal with one-input/one-output problems. This means if we end up looking at a function that involves more than one input, we must figure out how to reduce the amount of variables.

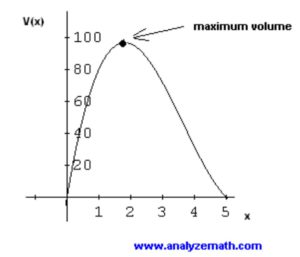
Now, let us look at the steps we should take to set up an optimization problem.

1. 1. Identify what is it that we need to optimize. Whether to maximize or minimize, the steps will be identical.
   2. Set up an equation relating the variables. This will be your optimization equation. The variable that you are trying to optimize should be the dependent variable. If you have not learned about implicit differentiation, make sure to rewrite the equation so that the dependent variable is the subject. If you understand how to apply implicit differentiation, you can leave the equation in implicit form.
   3. Identify whether any constraint is given in the question. Here is a rule of thumb about constraint: if the equation you have set up from step 2 has two or more independent variables, you must look for the constraint(s) that relate the multiple independent variables.
   4. Use the constraint to make one of the independent variables the subject, so you can replace the variable in your optimization equation.
   5. Once your optimization equation has only one independent variable, take the derivative of the equation in terms of the independent variable.
   6. The derivative is the rate of change in terms of the independent variable. When a function reaches its maximum or minimum, the rate of change is instantaneously stationary. In other words, the derivative would be 0. Set the derivative to 0 and solve for the independent variable. Be careful here if you have applied implicit differentiation to get to this point. You should ONLY replace the derivative of the dependent variable with 0 and nothing else.

Keep in mind that certain questions can be written in multiple parts that help you set up the problem accordingly. If that is the case, make sure to follow the individual parts to arrive at the answer.

Last but not least, verify whether your answer makes sense. Generally, if you receive only one solution from step 6, that should be the answer you are looking for. However, always read the question thoroughly to make sure you are providing the “correct” answer (you may need to use that solution to find another value). If you are getting multiple answers, here are a few things you can do to check which one is the correct solution:

1. 1. Look at the sign of the answer, could your solution be negative? Most optimization problems involve specific contexts, and nine times out of ten negative values would not make sense.
   2. If both solutions are positive, can both be realistic in terms of the context? Another trap answer is picking a number that is too large or too small. Put the number back into the constraint or the optimization equation and check to see whether the result makes sense or not.
   3. Use the first derivative test or second derivative test to verify whether the answer is a maximum or minimum.

 

---

About The Edge

The Edge Learning Center is Hong Kong’s premier Test Preparation, Academic Tutoring, and Admissions Consulting services provider. Founded in 2008, The Edge has helped thousands of students improve their ACT and SAT scores as well as their IB and AP grades. The AC team has just finished off another successful period in which students gained acceptance to schools such as Columbia, Yale, UChicago, and more! Check out our latest Admissions Results!