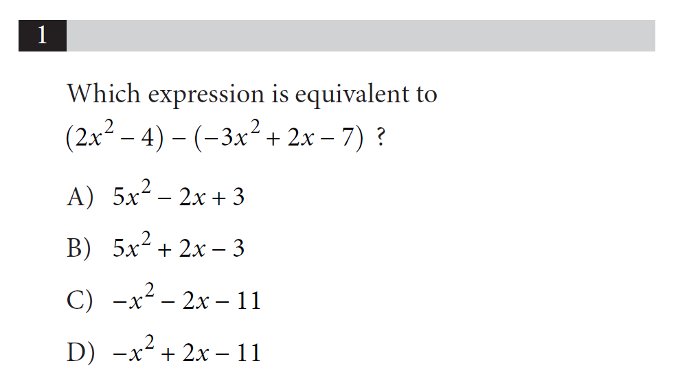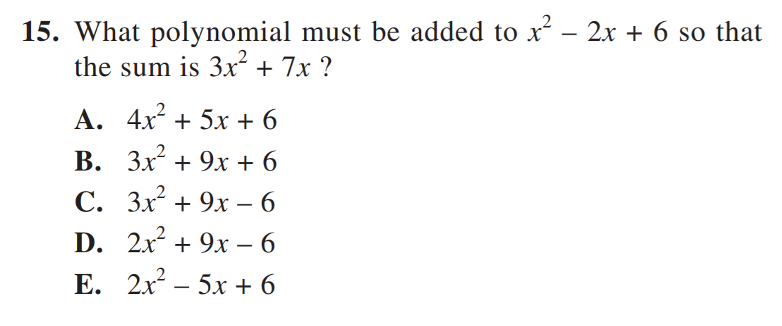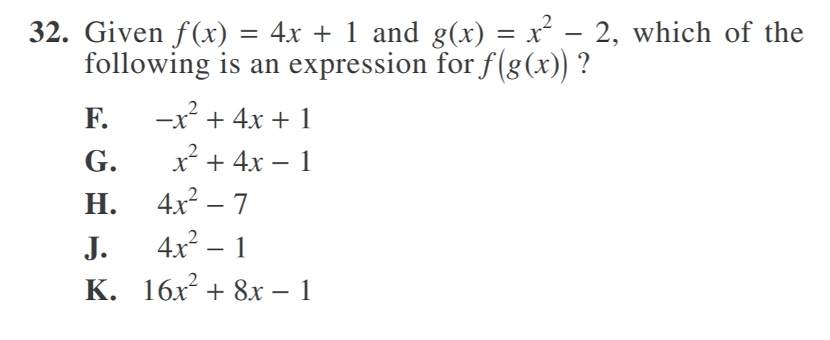Using a normal calculator to do Algebraic Expansion (Part 2)

By Owen Cheong 

(Math, Physics, Chemistry tutor at The Edge Learning Center)

In one of my previous articles, I talked about how to use a scientific calculator to perform algebraic manipulation. Please check it here before reading this article.

In part 2, I am going to show you how to apply this method in the SAT and ACT tests. I will use Casio fx-82ES Emulator to demonstrate how to use this technology to quickly solve algebraic questions. Don’t worry if you use a scientific calculator that is not Casio fx-82ES because every scientific calculator has a similar layout.

Before we use the trick, it is essential for us to use the substitution function in our calculators. We should first substitute 100 into the variable x before we do the following questions:

Let’s take a look at our first example:

[Example 1: SAT College Board Practice Test 6 Section 4 Q1]

After we make x becomes 100, we need to type the expression in the calculator:

To input x in your calculator, key in ‘alpha’ and ‘)’ in order. The output of the expression is 49803. The digits representing the constant term is ‘03’, which refers to 3, so the answer must be A.

[Example 2: ACT 2008-2009 Q6]

Similarly, we key in the expression to our calculator:

Now, let’s take a look at a more advanced example.

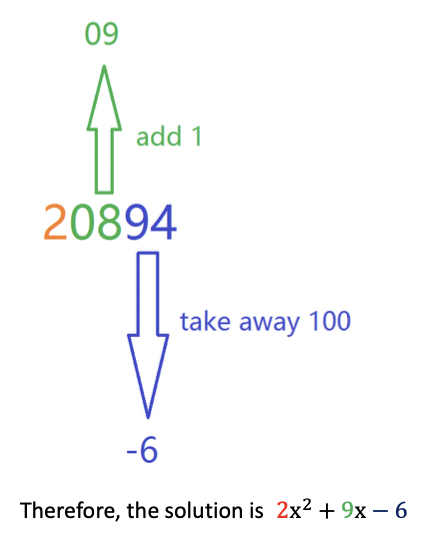
[Example 3: ACT 2005-2006 Q15]

To interpret the result ‘20894’, we need to apply the adjustment rule that I mentioned in my previous article:

Let’s check your understanding by answering the following questions!

[ACT 2010-2011 Q32]

Hint: You can already pick the correct solution after you figure out what is the constant term.

[SAT College Board Practice Test 3 Section 4 Q33 (free response)]

Suggestion: Find the values of a,b and c using the adjustment rule.

Blogs written: Winning a Nobel Prize by Solving ‘1+1’, Using a normal calculator to do Algebraic Expansion, 5 common mistakes made by IGCSE Math students, A guide to use online tools to perform mathematical modeling

About The Edge

The Edge Learning Center is Hong Kong’s premier Test Preparation, Academic Tutoring, and Admissions Consulting services provider. Founded in 2008, The Edge has helped thousands of students improve their ACT and SAT scores as well as their IB and AP grades. The AC team has just finished off another successful period in which students gained acceptance to schools such as Columbia, Yale, UChicago, UPenn, Oxford, and more! Check out our latest Admissions Results!