The Bernoulli Equation

Perhaps one of the most important laws of the natural world is the law of conservation energy, which in essence states that energy can neither be destroyed nor created. This fundamental principle helped the great Daniel Bernoulli first to deduce a relationship between pressure decrease and the corresponding fluid flow increase. Building upon the work of Bernoulli, the Swiss mathematician Leonhard Euler later expanded our understanding to incorporate the effect of a decrease in potential energy of the fluid and developed the famous equation we know today as the Bernoulli Equation.
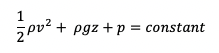
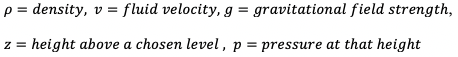
Whilst, the principles of the conservation of energy was vital in developing the Bernoulli Equation, you will notice that none of the constituent terms actually represent energy (in Jules), rather energy per volume, (Jm^(-3)). By multiplying the entire equation with volume, each of the terms would then expresses only energy, thus representing the conservation of energy.
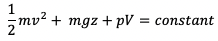
By multiplying ρ with volume, cancels out the volume component for the density, and thus resulting in mass (m). Correspondingly, each of the three terms would now represent: kinetic energy, gravitational potential energy and work done respectively.
This groundbreaking equation represents the overall energy for the continuous steady flow (when flow is not a function of time), with the sum of all these constituents remaining constant. Whilst this equation is very powerful, it is important to recognize that it only works under very ideal and specific conditions. First of all, the flow is isentropic, i.e. reversible, negligible turbulence, adiabatic (no net change in thermal energy). Finally, the simplified version of the Bernoulli equation that we are looking at also an important limitation, incompressible flow (material density is constant within a fluid parcel) meaning the velocity of the fluid is below Mach 1.
Bernoulli’s equation has many important applications, from understanding how a cricket ball swings in the air to deducing the exit velocity or pressure in a nozzle. However, the most famous application of this famous principle is in understanding the lift force in an airfoil. With the correct attack angle, the pressure on the top the airfoil would be greater than the pressure underneath. This pressure difference would cause result in an upward lift. Whilst Bernoulli’s equation can not explain why the fluid velocity is different dependent on which side of the foil it is, it can however be used to calculate what the difference velocities are. This is even more outstanding when considering the fact the equation was developed over a hundred years before the Wright brothers first achieved human flight.
About The Edge
The Edge Learning Center is Hong Kong’s premier Test Preparation, Academic Tutoring, and Admissions Consulting services provider. Founded in 2008, The Edge has helped thousands of students improve their ACT and SAT scores as well as their IB and AP grades. The AC team has just finished off another successful period in which students gained early acceptance to schools such as Columbia, MIT, UChicago, and more! Check out the rest of our 2019-2020 Admissions Results!

