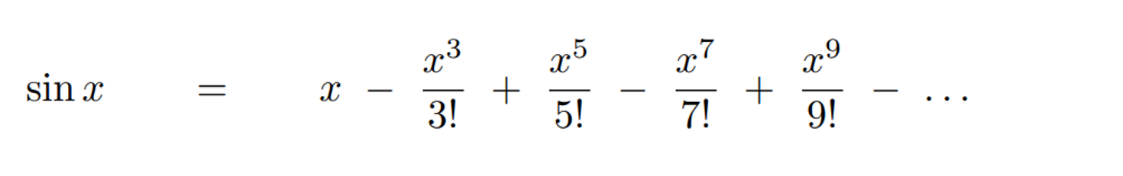How Does a Calculator Find Sine of an Angle?

By The Edge Learning Center 

In mathematics, one of the most important core skills is arithmetic. We learn about adding, subtracting, multiplying, and dividing at an early age. We learn that, as long as we persevere, these operations can be done without any calculator. We then evolve to learn about powers and roots. As the calculations become more complex, we begin to reply on a calculator to find the solutions. However, as difficult as these operations may become, they are still adding, subtracting, multiplying, and dividing at heart. When these operations are applied to variables, they are called algebraic operations. Solving problems involving these basic operations and unknowns is the core concept behind algebra, which is another important branch in mathematics.

At a certain point in our mathematical journey, we encounter new types of operations. Trigonometric functions like sine, cosine, and tangent are the most common “non-algebraic” functions we learn in math. They are non-algebraic (properly called transcendental functions) because we cannot calculate the result simply by using arithmetic (at least not with a finite number of calculations). In fact, with the exception of a few special angles, we have to reply on the calculator in order to find the result of sine, cosine, or tangent.

Before we learn about how a calculator finds the sine, cosine, or tangent of an angle, let us take a quick review of what trigonometric functions are. While most of us remember trigonometry solely as “SOHCAHTOA”, the true mechanics behind these functions are the ratios between the different sides of a right-angle triangle (here is a blog I wrote before about trigonometry). While we are eventually calculating the ratio between two numbers, which may seem like a simple division, the lengths of these triangles are rarely nice, rounded numbers. In fact, a calculator does not even consider finding the lengths when calculating trigonometric functions. Another important aspect about trigonometry is the angle. We learn about measuring angles in degrees, but a calculator must convert the angles to radians first before finding the result (here is another blog I wrote about degree and radian).

There are two things that we should note about this equation:

1. To find sine, we actually have to work with a polynomial, and
2. This polynomial is infinite. A calculator will only estimate an answer, so the more sophisticated our calculator is, the more decimal places it will be able to display. (For those of us who are unfamiliar with the exclamation mark used in this equation, I have another blog about the factorial function.)

The process of converting the sine function into the polynomial above is called the Taylor or Maclaurin series expansion; it is a useful tool that is taught in advanced calculus (students taking AP Calculus BC or Higher Level Analysis and Approach in IB will study this during the course).

Let us take a look at how we can now “calculate” sine of a random angle with a simple four-function calculator (one that can only do adding, subtracting, multiplying, and dividing).

We will first come up with an angle. Let us use 53°. For reference, the result of sine 53° is 0.79663551005… Since most questions will only require us to round to three significant figures, let us round it to 4 s.f. as comparison, which will give us a reference value of 0.7966.

Using only a standard four-function calculator, we will first convert the angle from degree to radian. To do so, we will need to multiply 53 by π, and then divide by 180. Since most four-function calculators will not have the number π readily available, we will estimate it using 3.14159. Thus, the angle in radian should be estimated as 0.925023722.

Next, we will apply the expansion. We will only work on the first three terms to see how close we are getting.

Finding the result of the factorials should be fairly straightforward even with a four-function calculator, as we just have to multiply one number at a time. In this case, 3! = 6, and 5! = 120.

The harder part is the power. Again, most four-function calculators do not have a “power” function. However, most of these calculators have a built-in short cut to find the result of a positive integer power. To do so, you press the multiplication button twice, and then press the equal sign “n” minus one times, where “n” is the power we are looking for. For example, to find 4⁵, we start with 4, then press multiple twice, and press equal four times. This way, we should get the following:

x = 0.925023722

x³=0.791514017

x⁵= 0.677273917

Finally, we calculate the result of the second and third term:

              2^nd term = 0.791514017 / 6 = 0.131919002

              3^rd term = 0.677273917 / 120 = 0.005643943

Putting all these terms together following the expansion, we have:

0.925023722 – 0.131919002 + 0.005643943 = 0.798748664

Compared to the rounded value of 0.7966 (4 s.f.), we can see that the result would likely be considered incorrect. This can be attributed to the rounding as we calculate each step and that we are only using three terms to estimate the answer.

In the end, it would make no sense of any of us to actually do this by hand. Calculators nowadays can crunch numbers in lightning speed, so we should just let them do the grunt work. What is interesting is that no matter how complicated or advanced a concept in mathematics can be, at its very core, it is still likely a bunch of arithmetic.